昨天看了cos，今天換個口味來看看sin吧！(怎麼一樣不太好吃)

跟著唸一遍！然後我們就直接開始吧！

寐偲，賽！！！

數學課時間

sin是一個角的正弦值，對於一個直角三角形的角來說就是對邊 / 斜邊

在圓上表示：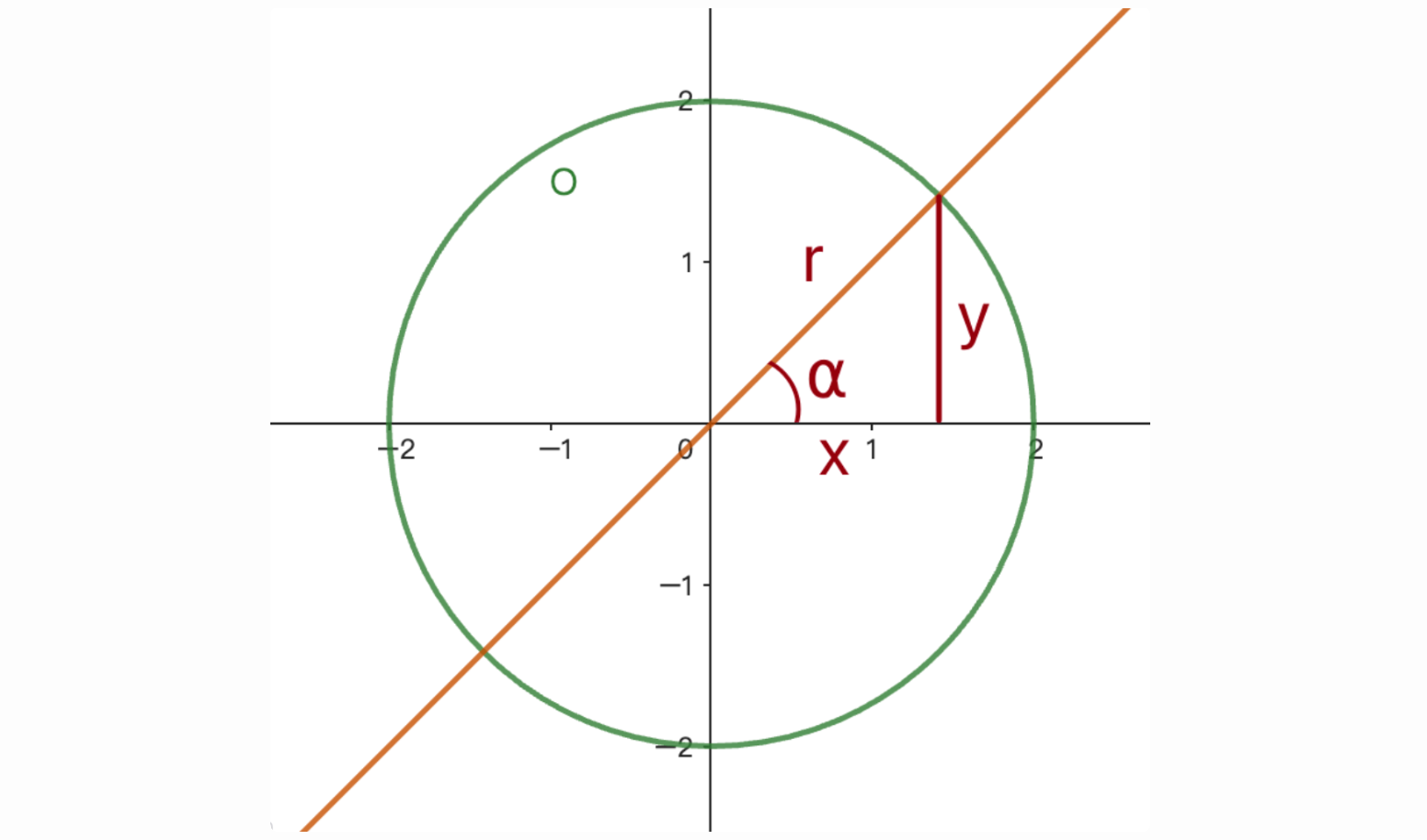

咦？怎麼又是你，但這次是sinα，所以值會是y / r

sin的值再某些特定角度的值較好觀察：

• sin0°(sin0) = 0
• sin90°(sinπ/2) = 1
• sin180°(sinπ) = 0
• sin270°(sin3π/2) = -1

來看y = sinx的圖形吧！同樣介於-1～1之間來回震盪，圖形跟y = cosx稍微錯開了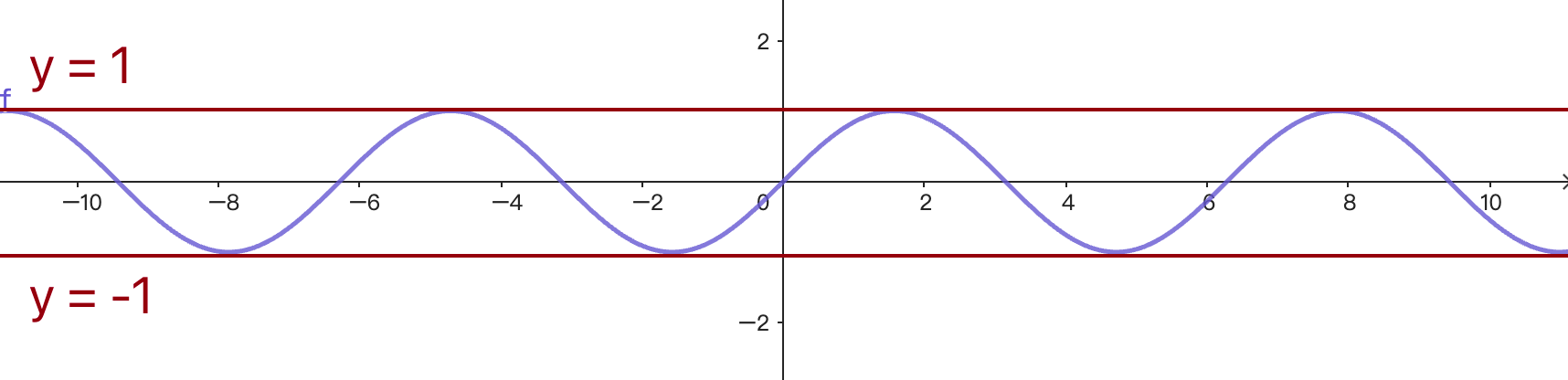

跟y = cosx放在一起比較：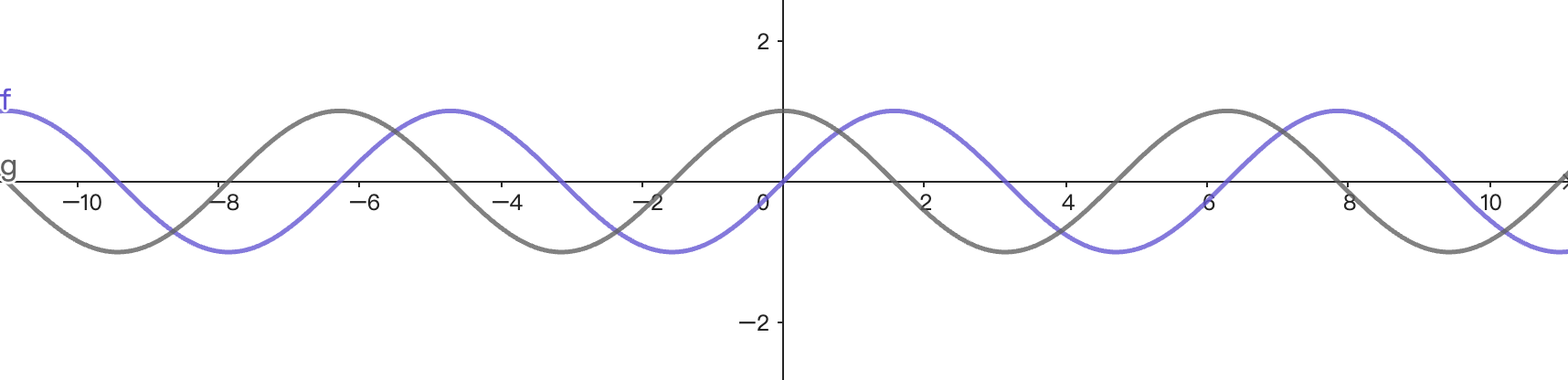

其實就是y = cosx的圖形水平移動π/2個單位。

既然他們圖長差不多，這方面的應用我也只想到類似cos做的漸變動畫。

但是！當cos跟sin湊在一起就能做一些很厲害的事情！！等我們介紹完語法再回頭來試試吧～

Math.sin()

語法

Math.sin(x)

參數

傳入一個以弧度表示的數值

回傳值

它會回傳x的sin（正弦）值，介於-1到1之間（含）。
如果x是Infinity、-Infinity或NaN，則回傳NaN。

規範

啊...都看完了，發現真cos不能說很像，只能說一模一樣。

Math.cos(0); //0
Math.cos(Math.PI / 2); //1
Math.cos(Math.PI); //1.2246467991473532e-16
Math.cos(Math.PI * 3 / 2); //-1

π代表著180°，JS提供了Math.PI來存放這個值（3.141592...）

這次只有sinπ的時候有誤差了，一樣測試看看：

const result = Math.sin(Math.PI);
console.log(Math.abs(result - 0) < Number.EPSILON ? 0 : result); //0

沒問題！

既然幾乎都一樣，那我們今天就到這邊吧！

應用

首先我們先理解一個圖：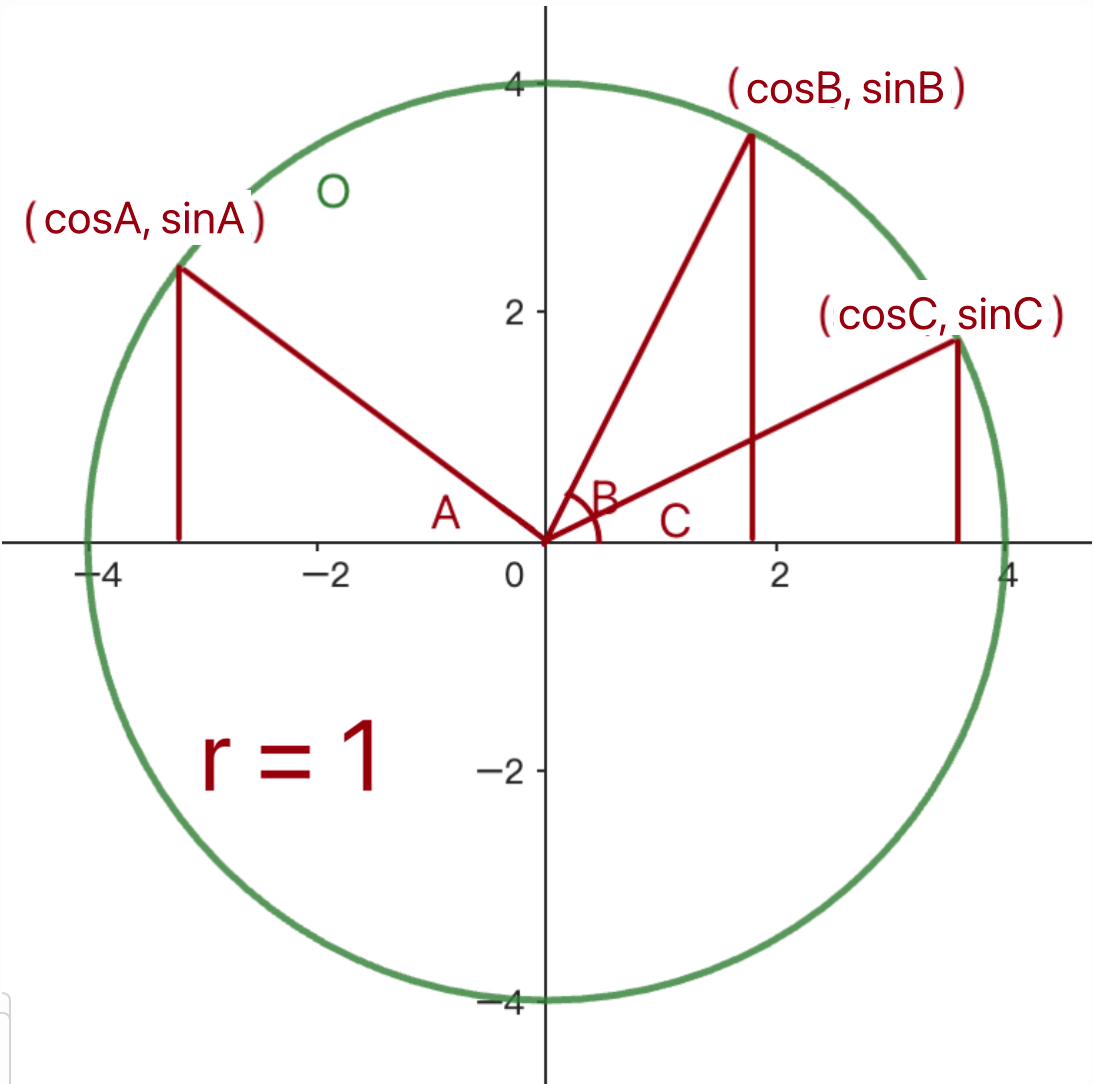

在半徑為1的圓上的每個點座標，我們都能用圓心角的sin跟cos值來表示他的(x, y)，因為半徑為1，所以x會是1 * cosθ，y就是1 * sinθ，所以座標就可以表示成(r * cosθ, r * sinθ)，那就讓我們來做兩顆行星繞恆星轉的動畫吧！

//HTML
<div class="planet"></div>
<div class="planet planetA"></div>
<div class="planet planetB"></div>

//CSS
.planet {
    position: absolute;
    top: 0;
    bottom: 0;
    left: 0;
    right: 0;
    margin: auto;
    width: 100px;
    height: 100px;
    border-radius: 100px;
    background-color: rgb(227, 215, 158);
}

.planetA {
    width: 50px;
    height: 50px;
    background-color: cadetblue;
}

.planetB {
    width: 30px;
    height: 30px;
    background-color: brown;
}

//JS
const planet = document.querySelector(".planet");
const planetA = document.querySelector(".planetA");
const planetB = document.querySelector(".planetB");

const translateA = {
    r: 200,
    x: 0,
    y: 0,
    a: 0,
};
const translateB = {
    r: 120,
    x: 0,
    y: 0,
    a: 0,
};
setInterval(() => {
    translateA.a++;
    translateA.x = translateA.r * Math.cos(translateA.a / 50);
    translateA.y = translateA.r * Math.sin(translateA.a / 50);
    planetA.style.transform = `translate(${translateA.x}px, ${translateA.y}px)`;
}, 16);

setInterval(() => {
    translateB.a++;
    translateB.x = translateB.r * Math.cos(translateB.a / 40);
    translateB.y = translateB.r * Math.sin(translateB.a / 40);
    planetB.style.transform = `translate(${translateB.x}px, ${translateB.y}px)`;
}, 16);

建立Translate物件來裝(r, x, y, a)四個值，分別代表（旋轉半徑、x座標、y座標、圓心角）
每16毫秒增加a的值，然後x, y再根據角度去更新位置，但每16毫秒角度+1會快到看不清楚，所以我把每次的角度a都再除以某個數來調整他角度增加的速度，這個部分大家可以再回去玩玩看～

結果：

今天比較特別，要讓行星動起來要多花點力氣，組合咒語：

寐偲，賽！！！
寐偲，摳賽！！！

因為時間有限，就只能簡單帶到這了，明天見！

source code：
https://github.com/860824jeremy/Math/tree/main/Math_sin

參考資料：

• MDN-Math.sin()
• ECMAScript-Math.sin()